Geometria y Composicion

Área de un triángulo rectángulo

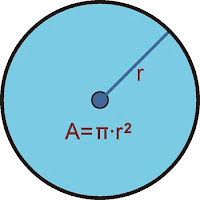
La fórmula para sacar el área de un circulo es: A = Π x r²

Área es igual a Pi por Radio al cuadrado.

Un POLÍGONO es una figura cerrada limitada por segmentos. Si todos los segmentos son iguales y, además, forman ángulos iguales, nos encontramos ante un POLÍGONO REGULAR.     Usando la REGLA y el COMPÁS, podemos construir POLÍGONOS REGULARES de cualquier número de lados, pero no todos tienen un procedimiento exacto. Podemos afirmar que, salvo alguna rara excepción, tienen un procedimiento exacto de construcción aquellos polígonos regulares en los que el valor de los ángulos es múltiplo de 3.     Para el resto, la única opción es emplear un procedimiento aproximado, es decir, inexacto, con algún pequeño error.     Tienen construcción exacta, por ejemplo, los polígonos regulares de 3, 4, 5, 6, 8, 10, 12, 15, 16, etc. lados.     No tienen construcción exacta, por ejemplo, los polígonos de 7, 9, 11, 13, 14, 18, etc. lados.     Constituye una excepción a la regla anteriormente dada el polígono de 17 lados, entre otros, para el cual existe un método exacto de construcción con regla y compás.

Método empírico.

·         Demostración geométrica.

1. Sea ADE el triángulo inscrito en la circunferencia y ABC el triángulo definido por la construcción de C. 2. Observando el ángulo en B: El punto medio de BC, E, determina un vértice del triángulo, pues BE=radio es el lado del exágono inscrito. 3. AE es una altura de ABC; luego OC=2·DM. 4. Trazando CD se define el punto P. Los triángulos POC y PMD son semejantes. 5. Como OBE es equilátero, OM=1/2·OB, luego OP=1/3·OB y por tanto AP=2/3·AB.

Luego la recta de la construcción que pasa por C y P (segunda división) coincide con la recta que pasa por C y D (vértice del triángulo). Al cortar en la circunferencia ambas construcciones, coincide D como vértice y como intersección de recta y circunferencia.

Método general

Se dibuja en primer lugar la circunferencia correspondiente. El problema se basa en dividir dicha circunferencia en tantas partes iguales como lados tenga el polígono que queremos trazar. Y este es un problema gráfico que no tiene solución general exacta.

Dividimos un diámetro de la circunferencia en tantas partes iguales como lados tenga el polígono, aplicando el teorema de Tales.

Numeramos de 0 a n. En nuestro ejemplo n=9, porque vamos a trazar un eneágono.

Trazamos dos arcos con centro en 0 y en 9 y radio el diámetro. Estos arcos se cortan en los puntos P y Q.

El segmento P2 corta a la circunferencia en el punto B. El arco 0B es la novena parte de la circunferencia, aproximadamente.

Obtenemos la misma medida si dibujamos el arco EF, trazando los segmentos P8 y Q8.

Trasladamos la magnitud del arco y dibujamos el polígono inscrito en la circunferencia de partida.

Para dibujar el polígono circunscrito a dicha circunferencia se trazan tangentes en cada uno de los puntos A, B, C... obtenidos.

Se realiza esta operación sea cual sea el valor de n.

 

Cuando el dato es el lado

Dibujamos el segmento AB, lado del polígono.

Dibujamos los arcos de radio AB con centros en A y en B. Trazamos la mediatriz y señalamos el punto 6. Con centro en 6 trazamos el arco AB de igual radio, que corta a la mediatriz en el punto 0. Dividimos 06 en seis partes iguales.

Si el polígono tiene 9 lados llevamos sobre la mediatriz, a partir del punto 6 tres unidades de las obtenidas al dividir AB y señalamos el punto 9. Con centro en 9 y radio 9A trazamos la circunferencia circunscrita al eneágono de lado AB.

Dibujamos el polígono.

Si queremos dibujar un polígono de n lados seguimos los mismos pasos y colocamos sobre la mediatriz unidades hasta alcanzar n, número de lados deseado. Así obtenemos el centro de la circunferencia circunscrita correspondiente, de radio nA.

Trazados particulares

Cuando el dato es el radio

Existen varias construcciones exactas coincidentes con las posibilidades gráficas de dividir un ángulo completo en partes iguales.

Podemos dibujar así: el triángulo equilátero (360º/3), el cuadrado (360º/4), el hexágono (360º/6), el dodecágono (360º/12) o el octógono (360º/8).

Si trazamos bisectrices de los ángulos obtenidos en cada caso hallaremos polígonos con el doble de lados. para trazos para el exagono debes hacer un circulo luego dividir en dos con una recta vertivcal y haciendo dos medias circuferencias trazando a los puntos opuestos

El heptágono regular de radio r

Existe una construcción aproximada del heptágono regular basada en que el lado del heptágono inscrito es aproximadamente igual a la altura del triángulo equilátero cuyo lado es el radio r.

Cuando el dato es el lado

Recordamos las construcciones del triángulo equilátero, el cuadrado y el hexágono regular a partir del lado.



El octógono regular se dibuja trazando la mediatriz de su lado y construyendo 45º por un extremo A del mismo. Se obtiene así el centro Q de la circunscrita al cuadrado de igual lado. La circunferencia de radio QA corta a la mediatriz en el centro O del octógono.

El pentágono regular

Las construcciones exactas del pentágono regular se deben a Hipócrates y se basan en la proporción áurea pues la razón entre la diagonal y el lado del pentágono es igual a Ф: d/l=Ф.

Vamos a ver cómo se realizan las construcciones y en el próximo capítulo, dedicado a la proporcionalidad directa, veremos las demostraciones correspondientes.

Cuando el dato es el la­­­­­­­­­­do AB: dibujamos el cuadrado de lado AB y la mediatriz de dicho lado. Con centro en N y radio NM trazamos un arco que corta a la prolongación de AB en el punto P. AP es la diagonal del pentágono, pues AP/AB=Ф.

Para construir el pentágono basta con realizar una triangulación colocando adecuadamente lados y diagonales.



Cuando el dato es el radio: Dibujamos la circunferencia circunscrita, hallamos la mediatriz de un diámetro y la de uno de los radios que contiene. Con centro en P y radio PA trazamos un arco que corta al diámetro en Q. El segmento PQ es el lado del pentágono inscrito.



Cuando el dato es la diagonal: Utilizamos otra construcción de la segmentación áurea. Por un extremo de d trazamos un segmento perpendicular de magnitud d/2 y dibujamos el triángulo rectángulo AMP de catetos d y d/2. Con centro en P y radio PH trazamos un arco que corta a la hipotenusa en el punto Q. Con centro en A trazamos un arco de radio AQ que corta a d en el punto B.

AB es el lado del pentágono regular de diagonal d, ya que d/AB=Ф.